0005最长回文子串

一、题目

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

1
2
3

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

1 2	输入：s = "cbbd" 输出："bb"

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

二、解题思路

本题最容易想到的一种方法应该就是中心扩散法。中心扩散法怎么去找回文串？

从每一个位置出发，向两边扩散即可。遇到不是回文的时候结束。

举个例子，str=acdbbdaa 我们需要寻找从第一个 b（位置为 3）出发最长回文串为多少。怎么寻找？

首先往左寻找与当期位置相同的字符，直到遇到不相等为止。
然后往右寻找与当期位置相同的字符，直到遇到不相等为止。
最后左右双向扩散，直到左和右不相等。如下图所示：

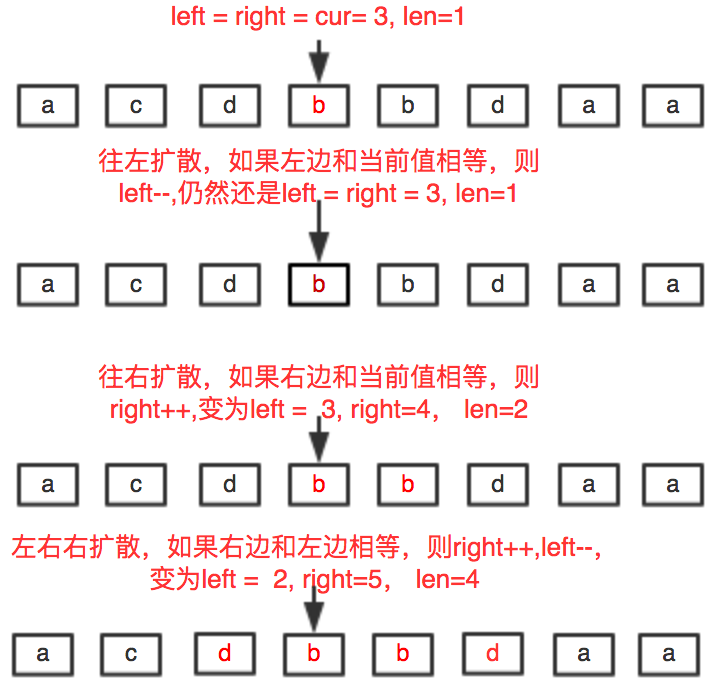
每个位置向两边扩散都会出现一个窗口大小（len）。如果 len>maxLen(用来表示最长回文串的长度）。则更新 maxLen 的值。

因为我们最后要返回的是具体子串，而不是长度，因此，还需要记录一下 maxLen 时的起始位置（maxStart），即此时还要 maxStart=len。

三、代码

class Solution {
        public String longestPalindrome(String s) {
            if (s == null || s.length() == 0) {
                return "";
            }
            int strLen = s.length();
            int left = 0;
            int right = 0;
            int len = 1;
            int maxStart = 0;
            int maxLen = 0;

            for (int i = 0; i < strLen; i++) {
                left = i - 1;
                right = i + 1;
                while (left >= 0 && s.charAt(left) == s.charAt(i)) {
                    len++;
                    left--;
                }
                while (right < strLen && s.charAt(right) == s.charAt(i)) {
                    len++;
                    right++;
                }
                while (left >= 0 && right < strLen && s.charAt(right) == s.charAt(left)) {
                    len = len + 2;
                    left--;
                    right++;
                }
                if (len > maxLen) {
                    maxLen = len;
                    maxStart = left;
                }
                len = 1;
            }
            return s.substring(maxStart + 1, maxStart + maxLen + 1);
        }
    }